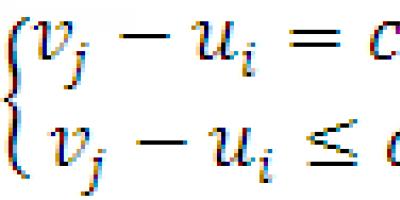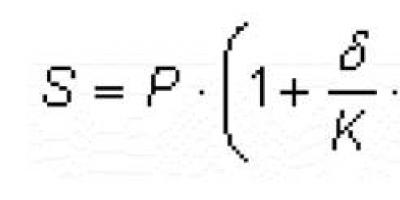Isto é, kas buvo pasakyta ankstesnėje pastraipoje, seka: Pagrindinio transporto problemos sprendimo optimumo criterijus: jei kokiam nors pagrindiniam transportavimo planui algebrinės tarifų sumos pagal ciklus visoms laisvoms ląstelėms yra neneigiamos, tai šis planas yra optimus.
Este método de reiškia, kaip rasti optimų problemas de transporte sprendimą, kuris susideda iš to, kad, turėdami tam tikrą pagrindinį sprendimą, jie apskaičiuoja algebrines visų laisvų ląstelių tarifų sumas. Jei optimumo kriterijus tenkinamas, tai šis sprendimas yra optimus; jei yra langelių su neigiamomis algebrinėmis tarifų sumomis, tada jie pereina prie naujo pagrindo, perskaičiuodami pagal ciklą, atitinkantį vieną iš tokių langelių. Tokiu būdu gautas naujas bazinis sprendimas bus geresnis už pirminį – jo įgyvendinimo kaštai bus mažesni. Naujam sprendimui taip pat patikrinamas optimumo kriterijaus tinkamumas ir, jei reikia, dar kartą atliekamas ciklo perskaičiavimas vienam iš langelių su neigiama algebrine tarifų suma ir pan.
Po tam tikro skaičiaus žingsnių jie pasiekia norimą optimų pagrindinį sprendimą.
Jei algebrinės visų laisvųjų langelių tarifų sumos yra teigiamos, turime unikalų idealų sprendimą; jei visų laisvųjų langelių algebrinės tarifų sumos yra neneigiamos, bet tarp jų yra algebrinių tarifų sumų, lygių nuliui, tada optimus sprendimas nėra vienintelis: perskaičiuojant per ciklą ląstelei su nuline algebrine tarifų sumą , gauname tą patį idealų sprendimą, bet rodapéą nuo pirminio (abiejų planų išlaidos bus vienodos).
Priklausomai nuo laisvų ląstelių tarifų algebrinių sumų apskaičiavimo metodų, yra du būdai optimiam transporto problemos sprendimui rasti:
Paskirstymo budas. Taikant šį metodą, kiekvienam tuščiam langeliui sukuriamas ciklas ir kiekvienam ciklui tiesiogiai apskaičiuojama algebrinė tarifų suma.
Métodos potenciais. Seu método de pirmiausia surandami bazių ir vartotojų potencialai, ou vėliau, naudojant potencialus, apskaičiuojama algebrinė tarifų suma kiekvienam tuščiam langeliui.
Potencialaus metodo pranašumai, lyginant su paskirstymo metodu, yra tai, kad nereikia konstruoti ciklų kiekvienam is tuščių langelių ir supaprastinamas algebrinių tarifų sumų skaičiavimas. Sukurtas tik vienas ciklas - tas, kuriuo atliekamas perskaičiavimas.
Naudodami potencialų metodą galime kalbėti ne apie algebrinių tarifų sumų ženklą, ou apie netiesioginių tarifų palyginimą su tikraisiais. Reikalavimas, kad algebrinės tarifų sumos mastų neneigiamos, pakeičiamas sąlyga, kad netiesioginiai tarifai neviršytų tikrųjų.
Reikėtų nepamiršti, kad potencialai (kaip ir ciklai) nustatomi iš naujo kiekvienai naujai bazinei linijai.
Aukščiau nagrinėjome uždarą problemas de transporte modeloį su teisinga pusiausvyra, kai tenkinama (1.3) sąlyga. Jei įvykdytas (1.4) (atviras modelis), transporte užduoties pusiausvyra gali būti sutrikdyta dviem kryptimis:
1. Atsargų kiekis išvykimo vietose viršija pateiktų paraiškų kiekį (transporto užduotis su atsargų pertekliumi):
a i > b j (kur i=1,...,m ; j=1,...,n);
2. Pateiktų paraiškų kiekis viršija turimus rezervus (problema de transporte su paraiškų pertekliumi):
ir aš< b j (где i=1,...,m ; j=1,...,n);
Panagrinėkime šiuos du atvejus paeiliui:
Problema de transporte dėl perteklinių atsargų.
Isso significa que há muitos problemas de transporte no seu balanço. Norėdami tai padaryti, be turimų n paskirties vietų B 1, B 2, ..., B n, pristatome dar vieną fiktyvią paskirties vietą B n +1, kuriai priskiriame fiktyvią užklausą, lygią atsargų pertekliui. prašymus
b n+1 = a i - b j (kur i=1,...,m ; j=1,...,n) ,
o transportavimo iš visų išvykimo taškų iki fiktyvios paskirties vietos b n +1 kaina bus laikoma lygi nuliui. Įvesdami fiktyvų tikslą B n +1 su jo prašymu b n +1, išlyginome transporto problemos pusiausvyrą ir dabar ją galima išspręsti kaip reguliaraus transporto problemą su teisingu balansu.
Problema de transporte dėl perteklinių užklausų.
Šią problemą galima sumažinti iki regulamenta problemas de transporte em teisingu balansu, jei įvesime fiktyvų išvykimo tašką A m +1 su atsargomis a m +1, lygiu trukstamoms atsargoms, ir transportavimo is fiktyvaus išvykimo taško kainą. į vistos paskirties vietas laikoma nuliu.
Bendra transporte problemas formuluotė susideda iš optimaus plano gabenti kai kuriuos vienarūšius krovinius iš eu išvykimo punktai (tiekėjai) A1, A2, . . ., A eu V n vartojimo taškai (vartotojai) B1, B2, . . . Bn taip, kad:
Pašalinti visus krovinius iš tiekėjų;
Patenkinti kiekvieno vartotojo poreikius;
Užtikrinti minimalias bendrąsias transporte išlaidas gabenant visa prekes.
Problema de transporte Apsvarstykite kaip optimumo kriterijus, kuris naudoja minimalias viso krovinio pervežimo išlaidas.
Pazymime:
ai - krovínio prieinamumas eu -asis išvykimo taškas https://pandia.ru/text/78/103/images/image205_0.gif" width="81" height="27 src=">;
сij - krovinio vieneto pervežimo išlaidos iš eu tarefa išvykimo j vartojimo vieta (taxas de transporte);
xij - iš vežamo krovinio kiekis eu tarefa išvykimo j tikslas, paskirties vieta, xij ≥ 0.
Os problemas de transporte matematinė formuluotė susideda iš neneigiamo tiesinių lygčių sistemos, kurioje tikslo funkcija turi mažiausią reikšmę, sprendimo.
Užrašykime matematinį transporto problemos modelį.
Būtina nustatyti matricą ), kuri atitinka šias sąlygas:
https://pandia.ru/text/78/103/images/image210_0.gif" width="74" height="45">.gif" width="47" height="21">.gif" width= "63" altura="20"> (5.3)
ir pateikia mažiausią tikslo funkcijos reikšmę
L () = https://pandia.ru/text/78/103/images/image215_0.gif" width="36" height="24"> atitinka tiesinių lygčių sistemą (5.1), (5.2) ir neneigiamumo sąlyga, Tai užtikrina reikiamo krovinio pristatymą kiekvienam vartotojui, turimų krovinių pašalinimą iš visų tiekėjų, ou taip pat eliminuoja grąžinimo transportavimą.
1 apibrėžimas. Bet koks neneigiamas tiesinių lygčių sistemų (5.1) ir (5.2), apibrėžtų matrica ), sprendinys vadinamas įgyvendinamas transporte problemas planos.
Apibrėžimas 2. Planas) https://pandia.ru/text/78/103/images/image218_0.gif" width="23" height="24">, vadinamas pagrindiniu arba nuoroda.
4 apibrėžimas. Jei atskaitos plane yra keletas nulinių kintamųjų verčių https://pandia.ru/text/78/103/images/image219_0.gif" width="55" height="22">.gif " width="55" height=" 22"> > , įvedama fiktyvi (n+ 1) paskirties vieta su reikalavimu mlrd+1 = – https://pandia.ru/text/78/103/images/image221_0.gif" width="83 height=22" height="22">
Jeigu< https://pandia.ru/text/78/103/images/image220_0.gif" width="56 height=25" height="25">.gif" largura="79" altura="22 src=">
Panagrinėkime vieną iš transporto problemos pirmojo atskaitos plan sudarymo būdų – minimalių sąnaudų metodą arba geriausią vieneto sąnaudų matricos elementą.
6 apibrėžimas. Geriausias vieneto kaštų (tarifų) matricos elementas bus mažiausias tarifas, jei užduotis bus nustatyta į tikslinės funkcijos mínimo, didžiausias tarifas – jei uždavinys nustatytas maximaliai.
Pirmojo atskaitos plano sudarymo algoritmos.
1. Tarp vieneto kaštų matricos randame geriausią tarifą.
2. Paskirstymo lentelės langelyje užpildykite pasirinktą tarifą su maximaliu galimu krovinio kiekiu, atsižvelgiant į eilučių ir stulpelių apribojimus. Tokiu atveju arba visas krovinys išimamas iš tiekėjo, arba visiškai patenkinami vartotojo poreikiai. Lentelės eilutė arba stulpelis išbraukiamas iš svarstymo ir toliau platinant nedalyvauja.
3. Iš likusių tarifų vėl išrenkame geriausią ir procesas tęsiasi tol, kol bus paskirstytas visa krovinys.
Se os problemas de transporte forem modelados, eles serão entregues com fiktyvus tiekėjas ou vartotojas, tada pirmiausia vykdomas paskirstymas tikriems tiekėjams ir vartotojams, ou galiausiai nepaskirstytas krovinys siunčiamas iš fiktyvaus tiekėjo arba fiktyviam Vartotojui.
Toliau tobuliname pirmąjį problemas de transporte etaloninį planeja ir gauname idealų planą naudojant potencialų metodą.
3 teoria . Transporte problemas planos ) yra optimus, jei yra skaičių ui ir vj (vadinamų potencialais) sistema (m + n), kuri tenkina sąlygas:
![]() (5.6)
(5.6)
![]() (5.7)
(5.7)
Possíveis problemas de transporte, problemas de transporte e problemas de transporte, kintamieji e žymi krovinio vieneto įvertinimą atitinkamai kilmės ir paskirties taškuose.
Pažymėkime: ) laisvos (neužimtos) lentelės langelio įvertį.
7 apibrėžimas. Os problemas de transporte são planos e ideais, mas você pode ver o que há de errado com o transporte (uždavinys nustatytas iki minimizeo).
Algoritmos de método potencial
1. Pirmojo etaloninio plano kūrimas problema de transporte naudojant minimalių sąnaudų metodą.
2. Plano išsigimimo tikrinimas .
Potenciali gali būti skaičiuojami tik neišsigimusio plano atveju. Jei atskaitos plane užimtų langelių skaičius (pagrindinių kintamųjų skaičius) yra mažesnis nei (m+n−1), tada viename iš laisvų lentelės langelių įrašome nulį, kad bendras užimtų langelių skai čius tampa lygus (m+n−1). Nulis įvedamas į Langelį su geriausiu tarifu, kuris priklauso eilutei ar stulpeliui. Sudarant pirmąjį orientacinį planą, kartu nubraukta. Šiuo atveju lentelės langelis, fiktyviai užimtas nuliu, neturėtų sudaryti uždaro stačiakampio kontūro su kitais užimtais lentelės langeliais.
3. Tikslo funkcijos reikšmės apskaičiavimas (5.4) susumavus tarifų sandaugas (vieneto sąnaudas) pagal pervežto krovinio tūrį visoms užimtoms lentelės ląstelėms.
4. Plano optimumo tikrinimas.
Mes nustatome potencialus. Kiekvienai užimtai ląstelei rašome lygtį, todėl gauname (m + n−1) lygčių sistema su (m + n) kintamaisiais.
Kadangi kintamųjų skaičius yra didesnis už lygčių skaičių, gauta sistema nėra apibrėžta ir turi begalinį sprendinių skaičių..gif" width="70" height="22">, tada likę potencialai nustatomi vienareikš miškai, ou jų reikšmės įrašomos į papildomą paskirstymo lentelių eilutę ir estupendo.
Kiekvienam laisvam langeliui nustatome įvertinimus https://pandia.ru/text/78/103/images/image233.gif" width="72 height=24" height="24">(problema išspręsta tikslo funkcijos mínimos), tada rastas optimus planas.Jei bent vienas laisvos langelio ivertis netenkina optimumo slygos, tai plana btina tobulinti perskirstan apkrov.
5.
Iš visų teigiamų laisvųjų langelių įverčių pasirenkame didžiausią (užduotis nustatyta iki minimizeo); iš visų neigiamų – didžiausia absoliučia reikšme (užduotis nustatyta maximaliai). Ląstelė, kuri atitinka aukščiausią balą, turi būti užpildyta, t. você. į ją turi buti siunčiama apkrova. Use o pasirinktą langelių, reikia pakeisti tiekimo apimtį, įrašytą daugelyje kitų užimtų langelių ir susietų su užpildomu, vadinamąjį ciklą.
Ciklas arba stačiakampis kontūras transporto uždavinio paskirstymo lentelėje yra trūkinė linija, kurios viršūnės yra užimtose lentelės langeliuose, ou nuorodos yra išilgai eilučių ir stulpelių bei kiekvie noje viršūnėje. ciclo yra lygiai dvi nuorodos, iš kurių viena yra eilutėje, kita stulpelyje . Jei ciklą sudaranti trukinė linija susikerta, tada susikirtimo taškai nėra viršūnės. Kiekvienai laisvai ląstelei galima sukurti vieną ciklą.
Ciklo viršūnės, pradedant nuo viršūnės, esančios pasirinktame pakrovimui langelyje, pakaitomis priskiriamos ženklais „+“ ou „-“. Šias ląsteles vadinsime pliusais ir minusais.
Iš krovinio tūrių minusinėse ląstelėse pasirenkame mažiausią ir pažymime jį θ. Perskirstome θ reikšmę išilgai kontūro, pridėdami θ prie atitinkamų krovinio tūrių pliuso langeliuose ir atimdami θ iš krovinio tūrių lentelės minuso langeliuose. Dėl to ląstelė, kuri buvo laisva ir pasirinkta įkelti, tampa užimta, ou viena iš užimtų kontūro langelių tampa laisva.
Patikriname gauto atskaitos plano optimumą, t.y. grįžtame į ketvirtą algoritmo etapą.
Macarrão.
1. Jeigu sukonstruoto ciklo minuso angeliuose yra dvi ar daugiau identiškų minimalių dydžių, tai perskirstan krovinių kiekius išleidžiama ne viena, ou dvi ar daugiau langelių. Tokiu atveju planas išsigimsta. Norint testou sprendimą, reikia užimti vieną ar daugiau vienu metu atlaisvintų lentelės langelių su nuliu, ou pirmenybė teikiama ląstelėms su geriausiu tarifu. Įvedama tiek nulių, kad naujai gautame atskaitos plane užimtų langelių (pagrindinių kintamųjų) skaičius būtų tiksliai (m + n−1).
2. Jeigu transporto uždavinio optimiame plane kurio nors laisvo langelio įvertis lygus nuliui), tai problema turi daug optimių planų. Ląstelėje, kurios balas nulinis, galite sukurti ciklą ir perskirstyti apkrovą. Dėl to gautas planas taip pat bus optimus ir turės tokią pačią tikslo funkcijos reikšmę.
3. Tikslo funkcijos reikšmę kiekvienoje iteracijoje galima apskaičiuoti taip:
(užduotis nustatyta iki mínimo),
(užduotis nustatyta maximaliai),
kur kontūru judančio krovinio tūris;
Laisvos ląstelės, į kurią nukreipiama apkrova, įvertinimas pereinant prie naujo etaloninio plano;
− tikslo funkcijos reikšmė k-oje iteracijoje;
− tikslo funkcijos reikšmė ankstesnėje iteracijoje.
Pavyzdys.
Trijuose didmeninės prekybos bazės sandėliuose yra vienarūšių krovinių po 40, 80 e 80 vnt. Šis krovinys turi būti gabenamas į keturias parduotuves, kurių kiekviena turi gauti atitinkamai 70, 20, 60 e 60 vnt. Pristatymo išlaidos vienam krovinio vienetui (tarifai) iš kiekvieno sandėlio ![]() ) vistos parduotuves
) vistos parduotuves ![]() ) pateikiami matriz
) pateikiami matriz  .
.
Sudaryti vienarūšių krovinių pervežimo minimaliomis transporto sąnaudomis planą (sąlyginiai skaičiai).
Aproveite.
1. Patikrinkime reikalingą ir pakankamą problemas sprendimo sąlygą:
40+80+80 = 200,
70+20+60+60 = 210.
Kaip matote, bendra krovinių paklausa viršija jo atsargas didmeninės prekybos bazės sandėliuose. Vadinasi, problemas de transporte modelis yra atviras ir neturi pirminės formos sprendimo. Modelo Norėdami gauti uždarą, pristatome papildomą (fiktyvų) sandėlį A4 su krovinių atsarga, lygia A 4 = 210 – 200 = 10 vnt. Darome prielaidą, kad krovinio vieneto gabenimo iš sandėlio A4 į visa parduotuves tarifai yra lygūs nuliui.
Visus pradinius duomenis įvedame į 7 lentelę.
Atsargos |
||||||||
|
A 1 | ||||||||
|
A 2 |  3 3
| |||||||
|
A 3 | ||||||||
|
A 4 | ||||||||
Poreikiai | 210 210 |
2. Pirmojo pamatinio plano sukūrimas naudojant minimalių išlaidų metodą.
Tarp tarifų mažiausias arba geriausias yra C14 = 1. Į Langelį A1B4 siunčiame didžiausią galimą apkrovą, lygią min(60,40) = 40. Tada x 14 = 40. Iš sandėlio A1 išvežtas visas krovinys, tačiau ketvirtos parduotuvės poreikis nepatenkintas 20 vnt. A1 é limpo e limpo.
Tarp likusių tarifų minimalus elementas C23 = 2. Krovinį min(60,80) = 60 siunčiame į Langelį A2B3. Seu atveju stulpelis B3 nenagrinėjamas, ou seu sandėlio A2 nepaimta 20 vnt.
Os elementos mínimos são os mínimos de C22 = 3. A2B2 é menor que apkrovą min(20,20) = 20. A segunda opção é A2 e o valor de B2 pode ser alterado.
Parenkame minimalų elementą C31 = 4. Į Langelį A3B1 siunčiame apkrovą, lygią min(70,80) = 70. Šiuo atveju į stulpelį B1 puresižvelgiama, ou iš sandėlio A3 nepaimta 10 vnt. Likusius krovinius é trečiojo sandėlio siunčiame į čiaupo angą A3B4, x 34 = 10. Ketvirtos parduotuvės paklausa nepatenkinama 10 vnt. às 10 horas. iš fiktyvaus tiekėjo - sandėlio A4. câmera de croviny A4B4, x 44 = 10.
De gaunamas pirmasis orientacinis planas, kuris yra priimtinas, nes visi kroviniai išvežti iš sandėlių ir patenkinti visų parduotuvių poreikiai.
3. Plano išsigimimo tikrinimas.
Pirmajame atskaitos plane užimtų langelių arba bazinių kintamųjų skaičius yra šeši. problemas de transporte planos e išsigimęs, nes pagrindinių kintamųjų skaičius nedegeneruotame plane lygus m + n – 1 = 4 + 4 – 1 = 7. Norint toliau spręsti problemą, reikia papildyti pamatinį planą įvedant fiktyvų transportą, t.y., u žimti vien ą iš laisvųjų su nuliniais angeliais .
Statant pirmąjį etaloninį planą, A2 eilutė e B2 stulpelis vienu metu buvo perbraukti, todėl planas išsigimė. Para que você possa imaginar que o valor A2 é definido e o valor B2 é válido, você precisa de tarifas mínimas e não precisa usar um acampamento fixo para usar as células. Os últimos são A2B4 e A3B2. Em langelį A2B4 siunčiame nulį.
4. Tikslinės funkcijos reikšmės apskaičiavimas.
Pirmojo etaloninio plano tikslinės funkcijos reikšmė nustatoma susumavus visų užimtų lentelės langelių tarifų ir vežamų krovinių apimčių sandaugą.
L(X1) = 4∙70 + 3∙20 + 2∙60 + 1∙40 + 3∙0 + 6∙10 + 0∙10 = 560 (tūkstantis rublių).
5. Optimalumo būklės tikrinimas.
Apskaičiuokime lentelės užimtų langelių potencialus pagal sąlygą: https://pandia.ru/text/78/103/images/image260_0.gif" width="139" height="22">Nuo nežinomo skaičiaus potencialai yra didesnis nei lygčių skai čius ( m + n > m + n – 1), tada imame vieną iš potencialų, lygių nuliui..gif" width="115 height=154" height="154">
Darant prielaidą, kad gausime https://pandia.ru/text/78/103/images/image265_0.gif" width="82" height="22">, ,https://pandia.ru/text/78/ 103 /images/image268_0.gif" largura="193" altura="22">
Apskaičiuotus potencialus įrašome į 7 lentelę. Apskaičiuokime laisvųjų langelių įverčius.
https://pandia.ru/text/78/103/images/image270_0.gif" largura="167" altura="22 src=">,
https://pandia.ru/text/78/103/images/image272_0.gif" largura="210" altura="22 src=">,
https://pandia.ru/text/78/103/images/image274_0.gif" largura="183" altura="22 src=">,
https://pandia.ru/text/78/103/images/image276_0.gif" largura="153" altura="22 src=">,
Pirmasis atskaitos planas nėra optimus, nes yra teigiamų laisvųjų langelių ir . Mes pasirenkame didžiausią teigiamą laisvos ląstelės įvertinimą - .
6. Naujo orientação plano kūrimas.
Ląstelėje A3B2 sukonstruosime stačiakampę uždarą grandinę (0 7 lentelė) e perskirstysime apkrovą grandinei. Kontūro viršūnės, pradedant nuo viršūnės, esančios laisvajame langelyje A3B2, pakaitomis priskiriamos ženklais „+“ ir „−“.
Iš krovinio tūrių minuso langeliuose pasirinkite mažiausią, t.y. θ = min(20,10) = 10. Pridėkite reikšmę θ = 10 prie krovinio tūrių pliuso langeliuose, atimkite iš krovinio tūrių minuso langeliuose uždarytuose. Kilpa. Dėl to gauname naują atskaitos planą, parodytą 8 lentelėje.
Sprendžiant transporto problemą, svarbus optimumo kriterijaus pasirinkimas. Kaip žinia, apytikslio plano ekonominio naudingumo įvertinimą gali lemti vienas ar kitas plano skaičiavimo pagrindas. Šis kriterijus yra ekonominis rodiklis, apibūdinantis plano kokybę. Iki šiol nėra visuotinai priimto vieno criterijaus, kuris visapusiškai atsižvelgtų į ekonominius veiksnius. Sprendžiant transporto problemą, optimumo kriterijumi įvairiais atvejais naudojami šie rodikliai:
1) Transporte darbų apimtis (kriterijus - atstumas t/km). Minimali rida yra patogi vertinant transportavimo planus, nes transportavimo atstumą galima lengvai ir tiksliai nustatyti bet kuria kryptimi. Se você considerar que o problema de transporte é negativo, suspeite o seu próximo transporte. Jis sėkmingai naudojamas sprendžiant kelių transporte problemas de transporte. Kuriant optimias vienarūšių krovinių vežimo transporto priemonėmis esquemas.
2) Tarifinis mokestis už krovinių gabenimą (kriterijus - gabenimo mokesčių tarifai). Leia o esquema de transporte gauti, kuri yra pati geriausia įmonės savarankiškų rodiklių požiūriu. Visi papildomi mokesčiai, taip pat esami lengvatiniai tarifai apsunkina naudojimą.
3) Eksploatacinės išlaidos kroviniams gabenti (kriterijus - veiklos sąnaudų kaina). Tiksliau atspindi pervežimo įvairiomis transporto rūšimis ekonomiškumą. Leidžia padaryti pagrįstas išvadas apie galimybę pereiti nuo vienos transporto rūšies į kitą.
4) Prekių pristatymo terminai (kriterijus – laiko sąnaudos).
5) Išlygintos sąnaudos (atsižvelgiant į eksploatavimo išlaidas, priklausomai nuo eismo dydžio ir investicijų į riedmenis).
6) Pateiktos sąnaudos (atsižvelgiant į vistos kapitalo investicijų į riedmenų įrenginių statybą eksploatacines išlaidas).
kur yra veiklos išlaidos,
Numatomas investicijų efektyvumo koeficientas,
Kapitalinės investicijos 1 tonai krovinio visame ruože,
T – kelionės laikas,
C – vienos tonos krovinio kaina.
Leidžia išsamiau įvertinti įvairių transportavimo planų varianteų racionalizavimą, gana išsamiai išreiškiant kiekybinę ir vienu metu kelių ekonominių veiksnių įtaką.
Panagrinėkime transporteo problemą, kurios optimumo criterijus yra minimalios viso krovinio pervežimo išlaidos. Krovinio vieneto gabenimo iš i-ojo išvykimo punkto į j-ąjį paskirties tašką tarifas pažymėkime – krovinio atsargas i-ajame išvykimo taške, – reikalavimus kroviniui i-oje išvykimo vietoje. j-asis paskirties taškas, ou iki – krovinių, pervežtų iš i-ojo išvykimo punkto į j-ąją paskirties vietą, skaičius. Tada matematinė problemas formuluotė susideda iš minimalios funkcijos reikšmės nustatymo
sąlygomis
Kadangi kintamieji atitinka tiesinių lygčių (2) ir (3) sistemas bei neneigiamumo sąlygą (4), užtikrinamas esamo krovinio išvežimas iš visų išvykimo taškų, reikiamo krovinio kiekio pristatymas į kiek vieną paskirties vietą , ir atgalinis transportas neįtraukiamas.
Taigi, T problema yra LP problema homem kintamųjų skaičius ir m+n apribojimų skaičius – lygybės.
Akivaizdu, kad bendras krovinių prieinamumas iš tiekėjų yra lygus , ou bendra krovinių paklausa paskirties vietose yra lygi vnt. Jeigu bendra krovinių paklausa paskirties vietose yra lygi krovinių pasiūlai pradinėse vietose, t.y.
tada vadinamas tokios transporte problemos modelis uzdaryta arba subalansuatas.
Se você tiver problemas praktinių, kai balanso sąlyga netenkinama. Tokie modeliai vadinami atviras. Galimi du atvejai:
Pirmuoju atveju visiškai patenkinti paklausą neįmanoma.
Tokia problema gali būti sumažinta iki įprasto transporto problemos taip. Jei paklausa viršija atsargas, t. você. fiktyvus ( eu+1)-tas išvykimo taškas su krovinio rezervu ir tarifai yra nuliniai:
Tada reikia sumažinti
sąlygomis
Dabar panagrinėkime antrąjį atvejį.
Panasiai, kai fiktyvus ( n+1) paskirties vieta su paklausa ir atitinkamais tarifas laikoma lygia nuliui:
Tada atitinkama T problema bus parašyta taip:
Sumažinti
tokiomis sąlygomis:
Esses problemas são resolvidos em termos de problemas de transporte, e os planos ideais são ótimos para resolver problemas planos.
Toliau apžvelgsime uždarą transporte problemas modeloį. Jei konkrečios problemos modelis yra atviras, tai remdamiesi tuo, kas išdėstyta aukščiau, uždavinio sąlygų lentelę perrašysime taip, kad būtų įvykdyta lygybė (5).
Kai kuriais atvejais reikia nurodyti, kad produktai negali buti gabenami tam tikrais maršrutais. Tada pervežimo šiais maršrutais kaštai nustatomi taip, kad viršytų didžiausias galimų transportavimo kaštus (kad būtų nuostolinga vežti nepasiekiamais maršrutais) – problemas esplêndidos mínimos. Maximaliai – atvirkščiai.
Kartais reikia atsižvelgti į tai, kad tarp kai kurių išsiuntimo vietų ir kai kurių vartojimo taškų buvo sudarytos sutartys dėl fiksuotų tiekimo kiekių, tada būtina toliau svarstyti garantuoto pristatymo apim tį. Norėdami tai padaryti, garantuoto tiekimo kiekis atimamas iš šių verčių:
· iš atitinkamo išsiuntimo punkto atsargų;
· pagal atitinkamos paskirties vietos poreikius.
Darbo Pabaiga -
O tema principal do skyriui:
Transporte Užduotis
Pavyzdys.. keturios tam tikro ekonominio regiono įmonės produkcijos gamybai..
Jei jums reikia papildomos medžiagos šia tema arba neradote to, ko ieškojote, rekomenduojame pasinaudoti paieška mūsų darbų duomenų bazėje:
Ką darysime su gauta medžiaga:
Jei ši medžiaga jums buvo naudinga, galite ją išsaugoti savo puslapyje socialiniuose tinkluose:
Parâmetros do projeto. Šis termina žymi nepriklausomus kintamuosius parametrus, kurie visiškai ir nedviprasmiškai lemia sprendžiamą projektavimo problemą. Os parâmetros do projeto são necessários para que o processo seja otimizado. Apostar que você está pagando por isso é o que você está procurando, naudojami kiekybiškai apibūdinti sistema, gali būti naudojami kaip projektavimo parametrai. Taigi, tai gali būti nežinomos ilgio, masės, laiko, temperatūros reikšmės. Os parâmetros do projeto são revelados e os problemas do projeto são sudėtingumo laipsnį. Paprastai projektinių parametrų skaičius žymimas n, ou patys projektiniai parametrai – x su atitinkamais indeksais. Taigi n šio uždavinio projetos de parâmetros de ônibus pažymėti
X1, X2, X3,...Xp.
Reikėtų pažymėti, kad projektiniai parametrai kai kuriuose šaltiniuose gali buti vadinami vidiniais kontroliuojamais parametrais.
Função Tikslinė. Tai išraiška, kurios vertę inžinierius siekia maximaliai arba minimaliai. Tikslinė funkcija leidžia kiekybiškai palyginti du alternatyvius sprendimus. Matematiniu požiūriu tikslo funkcija apibūdina tam tikrą (n+1) matmenų paviršių. Jo vertė nustatoma pagal projektinius parametrus
M = M (x1,x2,…,xn).
Inžinerinėje praktikoje dažnai sutinkamų objectktyvių funkcijų pavyzdžiai yra kaina, svoris, stiprumas, matmenys, efektyvumas. Jei projektinis parametras yra tik vienas, tai tikslo funkcija gali būti pavaizduota kreive plokštumoje (1 pav.). Se você tiver parâmetros de projeto, esse objeto funcional será usado como opção de paviršius trimatėje erdvėje (2 pav.). Esant trims ar daugiau projectavimo parametrų, tikslinės funkcijos nurodyti paviršiai vadinami hiperpaviršiais ir negali buti pavaizduoti įprastomis priemonėmis. Otimizamos o processo de maneira que você possa usar as funções de topologinės mais experientes, mas não é mais um recurso de eficácia do algoritmo pasirinkimas.
1 pav. Vienmatė tikslo funkcija.

2 pav. Dvimatė tikslo funkcija.
Tikslinė funkcija kai kuriais atvejais gali buti netikėčiausių formų. Pavyzdžiui, ji ne visada gali būti išreikšta uždara matematine forma; kitais atvejais tai gali masti atskira tiesinė funkcija. Norint nurodyti tikslo funkciją, kartais gali prireikti techninių duomenų lentelės (pavyzdžiui, vandens garų būklės lentelės) arba gali prireikti eksperimento. Kai kurias atvejais projektavimo parametrai ima tik sveikųjų skaičių. Pavyzdys galėtų būti dantų skaičius pavarų dėžėje arba varžtų skaičius flanše. Kartais dizaino parametrai turi tik dvi reikšmes – taip arba ne. Em kokybinius parametrus, tokius kaip prekę įsigijusio pirkėjo pasitenkinimas, patikimumas, estetika, optimizavimo procese sunku atsižvelgti, nes jų beveik neįmanoma apibūdinti kiekybiškai. Então, se você tiver uma forma de função de controle de tempo, ele será definido como um parâmetro de função de projeto nedviprasmiška.
Daugeliui optimizavimo problemų reikia įdiegti daugiau nei vieną tikslo funkciją. Os cartões vienas são jų gali masti nesuderinamas su kitu. Pavyzdys yra orlaivio konstrukcija, kai vienu metu reikalaujama didžiausio stiprumo, minimalaus svorio ir minimalių sąnaudų. Tokiais atvejais projektuotojas turi įvesti prioritetų system and kiekvienai tikslinei funkcijai priskirti tam tikrą bematį faktorių. De acordo com a “função de compromisso”, leidžianti optimizavimo proceso metu naudoti vieną sudėtinę tikslo funkciją.
Escolha o mínimo e o máximo. Vieni optimizavimo algoritmomai saiai surasti maximoą, kiti – surasti minimoą. Então, não há problemas extremos de tipo, você não precisa de um algoritmo específico, esse problema é sumaríssimo, o que é mais importante para o máximo de problemas paisagísticos, o pacote de funções é útil. Ši technika pavaizduota 3 pav.

3 pav. Kai minimalaus uždavinio tikslo funkcijos ženklas pasikeičia į priešingą, jis paverčia jį maximalia problema.
Dizaino erdvė. Tai yra srities, apibrėžtos visais n projektavimo parametrais, pavadinimas. Projektavimo erdvė nėra tokia didelė, kaip gali atrodyti, nes ją paprastai riboja daugybė sąlygų, susijusių su fisiniu problemas pobūdžiu. Apribojimai gali būti tokie stiprūs, kad problema neturės vieno patenkinamo sprendimo. Apribojimai skirstomi į dois grupos: apribojimai – lygybė e apribojimai – nelygybė.
Lygybės apribojimai – tai priklausomybės tarp projektavimo parametrų, į kurias reikia atsižvelgti ieškant sprendimo. Juose atsispindi gamtos dėsniai, ekonomika, teisė, vyraujantys skoniai ir reikalingų medžiagų prieinamumas. Apribojimų – lygybių skaičius gali masti bet koks. Jie atrodo kaip
C1 (X1, X2, X3,..., Xn) = 0,
C2 (X1, X2, X3, ..., X n) = 0,
..……………………………..
Cj(X1, X2, X 3,..., Xn) = 0.
Nelygybės apribojimai yra ypatingas apribojimų tipas, išreikštas nelygybėmis. Bendru atveju jų gali būti tiek, kiek norite, ir visi jie turi formą
z1 ?r1(X1, X2, X3,..., Xn) ?Z1
z2 ?r2(X1, X2, X3,..., Xn) ?Z2
………………………………………
zk ?rk(X1, X2, X3,..., Xn) ?Zk
Pažymėtina, kad labai dažnai dėl apribojimų ideali tikslo funkcijos reikšmė nepasiekiama ten, kur jos paviršius turi nulinį gradienteą. Dažnai geriausias sprendimas atitinka vieną is projectavimo erdvės ribų.
Tiesioginiai ir funkciniai apribojimai. Tiesioginiai apribojimai turi formą
xni? XI? xvi não é? ,
čia xнi, xвi yra mažiausios ir didžiausios leistinos i-ojo valdomo parametro reikšmės; n yra valdomų parametrų erdvės matmuo. Pavyzdžiui, daugelio objectų elementų parametrai negali buti neigiami: xнi ? 0 (geometriniai matmenys, elektrinė varža, masė ir kt.).
Funkciniai apribojimai, kaip taisyklė, reiškia išvesties parametrų, kurie nėra įtraukti į tikslinę funkciją, veikimo sąlygas. Funkciniai apribojimai gali būti:
- 1) dicas lygybių
- c(X) = 0; (2.1)
- 2) dicas nelygybių
tz (X) › 0, (2.2)
kur w(X) e q(X) são funções vetoriais.
Tiesioginiai ir funkciniai apribojimai sudaro leistiną paieškos sritį:
ХД = (Х | w(Х) = 0, ц (Х)›0, xi › xнi ,
xi ‹ xвi už i ? ).
Jei apribojimai (2.1) ir (2.2) sutampa su veikimo sąlygomis, tada leistina sritis dar vadinama XP veikimo sritimi.
Bet kuris iš kompaktiniam diskui priklausančių taškų X yra įmanomas problemos sprendimas. Parametrinė sintezė dažnai keliama kaip bet kokių galimų sprendimų nustatymo problema. Tačiau daug svarbiau yra išspręsti optimizavimo problemą – rasti optimų sprendimą tarp galimų.
Vietinis optimumas. Tai yra taško projectavimo erdvėje pavadinimas, kuriame tikslinė funkcija turi didžiausią vertę, palyginti su jos vertėmis visuose kituose taškuose, esančiuose šalia jos. 4 paveiksle parodyta vienmatė tikslo funkcija, turinti du vietinius optimius. Dažnai projektavimo erdvėje yra daug vietinių idealų, todėl reikia stengtis, kad pirmasis nebūtų klaidingas dėl optimaus problemos sprendimo.

4 pav. Savavališka tikslo funkcija gali turėti keletą lokalinių idealų.
Pasaulinis optimumas yra optimus sprendimas visai dizaino erdvei. Jis yra geresnis už visus kitus sprendimus, atitinkančius vietinius optimus, ir būtent tai yra tai, ko dizaineris ieško. Gali būti, kad rodapés projektavimo erdvės dalyse yra keletas vienodų globalių optimų. Esta variante é considerada uma variante otimizada, mas a função é remiantis. Tokiu atveju dizaineris gali pasirinkti parinktį intuityviai arba remdamasis gautų varianteų palyginimu.
Criterijų parinkimas. A resolução de problemas não tem problemas extremos e funciona de forma simples. As funções básicas são muito fáceis de usar, e os objetos técnicos que você pode usar são os vetores mais adequados para a criação ideal (daugiakriterijų). Seja para, patobulinus vieną iš išvesties parametrų, kaip taisyklė, pablogėja kitas, nes visi išvesties parametrai yra tų pačių valdomų parametrų funkcijos ir negali keistis nepriklausomai vienas nuo kito. Tokie išvesties parametrai vadinami konfliktiniais parametrais.
Turi būti viena tikslinė funkcija (unikalumo principas). Kelių kriterijų problemas redukavimas iki vieno kriterijaus uždavinio vadinamas vektorinio kriterijaus konvoliucija. Use as surasti jo ekstremumą sumažinama iki matematinio programavimo problemos. Atsižvelgiant į tai, kaip skaliarinėje kokybės funkcijoje parenkami e derinami išvesties parametrai, išskiriami daliniai, adityviniai, dauginamieji, minimalūs, estatísticas kriterijai ir kiti kriterijai. O objeto técnico do projeto é a técnica específica dos parâmetros de configuração necessários. Šie reikalavimai išreiškiami konkrečiais skaitiniais duomenimis, jų kitimo diapazonu, eksploatavimo sąlygomis ir priimtinomis mažiausiomis arba didžiausiomis vertėmis. Reikalingi ryšiai tarp išvesties parametrų ir techninių reikalavimų (TR) vadinami veikimo sąlygomis ir rašomi tokia form:
sim< TTi , i О ; yi >TTj, jO;
ano = TTr ± ?ano; ro.
kur yi, yj, yr - išvesties parametrų rinkinys;
TTi, TTj, TTr - reikalingos atitinkamų išvesties parametrų kiekybinės vertės pagal technines specifikacijas;
Yr – leistinas r-ojo išėjimo parametro nuokrypis nuo techninėse specifikacijose nurodytos TTr reikšmės.
Exploatacinės sąlygos turi lemiamą reikšmę kuriant techninius prietaisus, nes projektavimo užduotis yra parinkti tokį projektinį sprendimą, kuriame visos exploatavimo sąlygos butų geriausiai tenkinamos per visą išor este parâmetro pokyčių diapazoną ir kai tenkinami visi techninių specifikacijų reikalavimai. .
Konkretūs kriterijai gali būti naudojami tais atvejais, kai tarp išvesties parametrų galima išskirti vieną pagrindinį parametrą yi(X), kuris labiausiai atspindi projektuojamo objeto efektyvumą. Esses parâmetros funcionam normalmente. Esses parâmetros são pavyzdžiai: objeto de energia – galia, tecnologia de máquina – našumas, transporte priemonei – keliamoji galia. Os parâmetros técnicos do objeto são os mesmos. Visų kitų objeto išvesties parametrų veikimo sąlygos vadinamos funkciniais apribojimais. Otimizavimas, pagrįstas tokia formuluote, vadinamas optimizavimu pagal tam tikrą kriterijų.
Seu método privalumas yra jo paprastumas, reikšmingas trukumas yra tai, kad didelę naudingumo ribą galima gauti tik pagrindiniam parametrui, kuris yra priimtas kaip tikslinė funkcija, ou kiti išvesties parametrai neturės jokių ribinių dyd žių.
Svertinio priedo kriterijus naudojamas tada, kai exploatacinės sąlygos leidžia atskirti dvi išėjimo parametrų grupos. Pirmoji grupė apima išvesties parametrus, kurių reikšmės optimizavimo proceso metu turėtų būti padidintos y+i(X) (našumas, atsparumas triukšmui, veikimo be gedimų tikimybė ir kt.), antroji grupė – išėjimo parametra i, kurių vertės tur ėtų būti sumažintos y-i (X ) (kuro sąnaudos, pereinamojo proceso trukmė, viršijimas, poslinkis ir kt.). Sujungus kelis išvesties parametrus, kurie paprastai turi rodapé fizinius matmenis, į vieną skaliarinę tikslo funkciją, reikia iš anksto normalizuoti šiuos parametrus. Toliau bus aptariami parametrų normalizavimo metodai. Kol kas darysime prielaidą, kad visi y(X) yra bedimensiniai ir tarp jų nėra tokių, kurie atitiktų lygybės tipo veikimo sąlygas. Tada tikslo funkcijos sumažinimo atveju vektoriaus kriterijaus konvoliucija bus tokia forma
kur aj>0 yra svertinis koeficientas, nulemiantis j-ojo išvesties parametro svarbos laipsnį (dažniausiai aj pasirenka projektuotojas ir optimizavimo processo metu išlieka pastovus).
A forma de função principal (2.1) é a seguinte: os critérios de adityvinį, gali būti rašoma ir tuo atveju, kai visos arba pagrindinės atlikimo sąlygos turi lygybių formą. Tada tikslo funkcija
nustato yj(X) vidutinį kvadratinį artėjimą prie pateiktų techninių reikalavimų TTj.
Dauginimo kriterijus galima naudoti tais atvejais, kai nėra lygybės tipo veikimo sąlygų e išvesties parametrai negali turėti nulinių reikšmių. Tada multiplikacinė tikslo funkcija, kurią reikia sumažinti, turi formą
Vienas reikšmingiausių tiek adityvinių, tiek dauginamųjų kriterijų trūkumų yra tai, kad formuluojant problemą cleansižvelgta į techninius reikalavimus išvesties parametrams.
Funkcijų formos kriterijus naudojamas, kai užduotyje nustatytas geriausios nurodytos (atskaitos) charakteristikos yCT(X, y) atitikimas su atitinkama projektuojamo objeto išvesties charakteristika y(X, y), kur y yra koks nors kintamasis , pavyzdžiui, da žnis, laikas, pasirinktas fazės kintamasis . Šios užduotys apima: automatinės valdymo sistemos, kuri užtikrina reikiamo tipo pereinamąjį procesą kontroliuojamam parametrui, projektavimą; tranzistoriaus modelio parametrų, užtikrinančių maximalų sutapimą tarp jo teorinių srovės-įtampos charakteristikų ir experimentinių, nustatymas; ieškoti sijų sekcijų parametrų, kurių reikšmės geriausiai sutampa su pateiktą įtempių diagramą su apskaičiuotąja ir kt.
Tam tikro optimizavimo kriterijaus naudojimas šiais atvejais susijęs su nuolatinių charakteristikų pakeitimu baigtiniu mazginių taškų rinkiniu ir vienos iš šių tikslinių funkcijų, kurias reikia sumažinti, pasirinkima s:

čia p – mazginių taškų uj skaičius kintamojo u ašyje; aj - svoriniai koeficientai, kurių reikšmės yra didesnės, tuo mažesnis nuokrypis y(X, φj) - yTT(X, φj) turi būti gautas j-ajame taške.
Maximin (minimax) é um fator de segurança que é ideal para o uso de tikslų – kuo geriau patenkinti exksploatacines sąlygas.
Įveskime kiekybinį j-osios veiklos sąlygos įvykdymo laipsnio įvertinimą, pažymime zj ir pavadinkime parâmetro yj našumo rezervu. J-ojo išvesties parametro paraštės apskaičiavimas gali būti atliekamas įvairiais būdais, pavyzdžiui,
čia aj yra svorio koeficientas; yjnom - vardinė j-ojo išėjimo parametro vertė; dj yra reikšmė, apibūdinanti j-ojo išvesties parâmetro sklaidą.
Čia daroma prielaida, kad visi santykiai redukuojami iki formos yi< TТj. Если yi >TTj, tada-yj< -TТj . Следует принимать аj >1 (rekomenduojamos reikšmės 5 ? aj ? 20), jei norima pasiekti j-ąjį techninį reikalavimą su tam tikra paklaida, t. você. yj = TTj ± ?yj; aj=l, jei reikia gauti didžiausią įmanomą įvertį zj.
Os sistemas técnicos são muito úteis para definir parâmetros vetoriais, taigi e vetores Z=(zm,zm,…,zm). Todėl tikslinė funkcija turėtų būti suformuota kaip kokia nors vertinimo vektoriaus funkcija μ(Z). Pavyzdžiui, jei tikslinė funkcija laiko tik to išvesties parametro rezervą, kuris tam tikrame taške X yra pats blogiausias techninių specifikacijų reikalavimų tenkinimo požiūriu, tada
čia m – darbingumo rezervų skaičius.
Dabar natūralu iškelti tokią paieškos strategiją X, kuri maximaliai padidintų rezervų mínimoą, t.y.
kur HD yra paieškos sritis.
Otimizavimo kriterijus su tikslo funkcija (2.6) vadinamas maximalaus kriterijumi.
Critérios estatísticos. Otimizavimas naudojant statistinius kriterijus yra saias gauti maximalią našumo tikimybę P. Ši tikimybė laikoma tiksline funkcija. Tada me turime problemą
Valdomųjų ir išėjimo parâmetros normalizavimas. Valdomųjų parametrų erdvė yra metrinė. Todėl, renkantis paieškos žingsnių kryptis ir reikšmes, būtina įvesti vienokią ar kitokią normą, identifikuojamą su atstumu tarp dviejų taškų. Pastaroji daro prielaidą, kad visi valdomi parametrai turi tą patį matmenį arba yra be matmenų.
Galimi įvairūs normavimo būdai. Kaip pavyzdį apsvarstykite logaritminio normalizavimo metodą, kurio pranašumas yra perėjimas nuo absoliučių parametrų prieaugių prie santykinių. Šiuo atveju i ir valdomas parametras ui paverčiamas bedimensiniu xi taip:
kur oi yra koeficientas, skaičiais lygus parametro ui vienetui.
Išėjimo parametrų normalizavimas gali būti atliekamas naudojant svorinius koeficientus, kaip ir adityviniame kriterijuje, arba pereinant nuo yj prie našumo rezervų zj pagal (2.5).